Rechte, saaie, scherpe en uitgevouwen hoek
Laten we beginnen met te bepalen wat een hoek is. Ten eerste is het een geometrische figuur. Ten tweede wordt het gevormd door twee stralen, die de zijden van de hoek worden genoemd. Ten derde komen de laatste uit een punt, dat de hoekpunt van de hoek wordt genoemd. Uitgaande van deze tekens, kunnen we een definitie maken: een hoek is een geometrische figuur, die bestaat uit twee stralen (zijden) die uit een enkel punt (vertex) komen.
Ze worden ingedeeld naar graad, naar locatie ten opzichte van elkaar en ten opzichte van de omtrek. Laten we beginnen met de soorten hoeken op basis van hun grootte.
Er zijn er verschillende. Laten we elke soort in meer detail bekijken.
De hoofdtypen van hoeken zijn slechts vier - een rechte, stompe, scherpe en uitgevouwen hoek.
rechtdoor
Het ziet er als volgt uit:

De graadmaatregel is altijd 90overmet andere woorden, een rechte hoek is een hoek van 90 graden. Alleen bevinden ze zich in zulke vierhoeken als een vierkant en een rechthoek.
dof
Het ziet er als volgt uit:
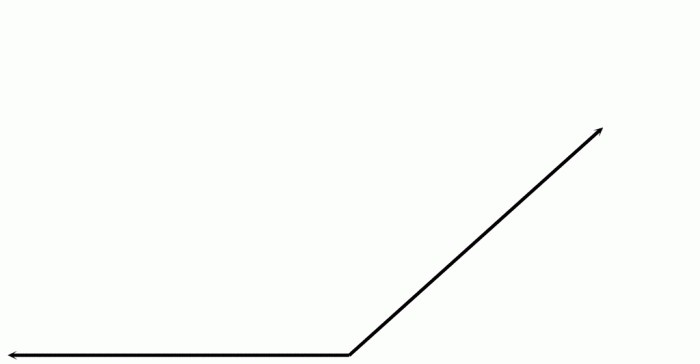
De mate van een stompe hoek is altijd groter dan 90over, maar minder dan 180over. Het kan voorkomen in vierhoeken als een ruit, een willekeurig parallellogram in veelhoeken.
scherp
Het ziet er als volgt uit:

De maat van de scherpe hoek is altijd minder dan 90over. Het komt voor in alle vierhoeken behalve een vierkant en een willekeurig parallellogram.
ingezet
De opengevouwen hoek is als volgt:

In polygonen komt het niet voor, maar niet minder danbelangrijker dan alle anderen. De opengevouwen hoek is een geometrische figuur, waarvan de mate altijd 180º is. Hierop is het mogelijk om aangrenzende hoeken te construeren, die van zijn bovenste een of meerdere stralen in elke richting zijn getrokken.
Er zijn verschillende secundaire soorten hoeken. Ze worden niet op scholen bestudeerd, maar moeten wel weten wat hun bestaan is. Er zijn slechts vijf kleine hoeken:
1. Nul
Het ziet er als volgt uit:

De echte naam van de hoek spreekt al over zijn omvang. Het interne gebied is 0overen de zijkanten op elkaar liggen zoals weergegeven in de figuur.
2. De schuine
De schuine kant kan recht en stom en scherp zijn en uitgevouwen. De belangrijkste voorwaarde is dat deze niet 0 mag zijnover, 90over, 180over, 270over.
3. Convex
Convex zijn nul, rechte, stompe, scherpe en ongevouwen hoeken. Zoals je al begreep, is de graadmaat voor de convexe hoek 0over tot 180over.
4. Niet-convex
Niet-convex zijn hoeken met gradenmaat vanaf 181over tot 359over inclusive.
5. Vol
Volledig is de hoek met gradenmaat 360over.
Dit zijn allemaal soorten hoeken op basis van hun grootte. Bekijk nu hun mening over de locatie in het vlak ten opzichte van elkaar.
1. Extra

Dit zijn twee scherpe hoeken die één rechte lijn vormen, d.w.z. hun som is 90over.
2. Gerelateerd

Aangrenzende hoeken worden gevormd als deze via een ontwikkelde, meer in het bijzonder, door zijn top, een straal in elke richting houden. Hun som is 180over.
3. Verticaal

Verticale hoeken worden gevormd wanneer twee rechte lijnen elkaar kruisen. Hun graadmaatregelen zijn gelijk.
Ga nu naar de soorten hoeken die zich ten opzichte van de cirkel bevinden. Er zijn er maar twee: centraal en ingeschreven.
1. De centrale

De middelpunt is de hoek met de vertex in het midden van de cirkel. De graadmaat is gelijk aan de mate van een kleinere boog, verbonden door de zijkanten.
2. Ingeschreven
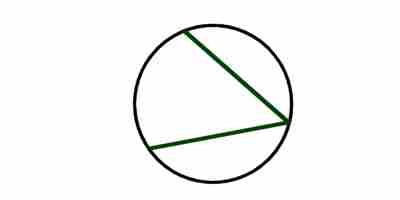
Ingeschreven is de hoek waarvan de top op de cirkel ligt en waarvan de zijkanten elkaar kruisen. De graadmaat is gelijk aan de helft van de boog waarop hij rust.
Dat draait allemaal om hoeken. Nu weet je dat naast de meest bekende - scherp, stomp, direct en gedetailleerd - er veel andere soorten geometrie in geometrie zijn.







