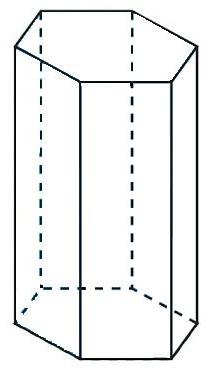
Hoe de hoogte te vinden in een gelijkbenige driehoek? De vindingformule, de hoogte-eigenschappen in een gelijkbenige driehoek

Geometrie is niet alleen een object op school,die een uitstekende beoordeling moet krijgen. Het is ook kennis die vaak nodig is in het leven. Als u bijvoorbeeld een huis met een hoog dak wilt bouwen, moet u de dikte van de stammen en hun aantal berekenen. Dit is gemakkelijk als je de hoogte weet te vinden in een gelijkbenige driehoek. Architecturale structuren zijn gebaseerd op kennis van de eigenschappen van geometrische vormen. De vormen van gebouwen lijken vaak visueel op hen. De Egyptische piramiden, pakjes met melk, artistiek borduurwerk, noordelijke schilderijen en zelfs pasteitjes zijn allemaal driehoeken rondom een ​​persoon. Zoals Plato zei, de hele wereld is gebaseerd op driehoeken.

De gelijkbenige driehoek

Om het duidelijker te maken, wat hierna zal worden besproken, is het de moeite waard om de basisbeginselen van de geometrie te onthouden.

Een driehoek is gelijkbenig als deze twee gelijke zijden heeft. Ze worden altijd lateraal genoemd. De zijde, waarvan de afmetingen verschillen, werd het terrein genoemd.

Basisbegrippen

Zoals elke wetenschap heeft geometrie zijn eigen basisregels en concepten. Er zijn veel van hen. Overweeg alleen degenen zonder wie ons onderwerp enigszins onbegrijpelijk zal zijn.

De hoogte is een rechte lijn loodrecht op de andere kant.

De mediaan is een segment dat van een hoekpunt van de driehoek is gericht, uitsluitend naar het midden van de andere kant.

De bissectrice is een balk die de hoek in twee deelt.

De bissectrice van een driehoek is een rechte lijn, of beter gezegd, een deel van de bissectrice van de hoek die de top met de andere kant verbindt.

Het is heel belangrijk om te onthouden dat de bissectrice van de hoek noodzakelijkerwijs een straal is en dat de bissectrice van een driehoek deel uitmaakt van een dergelijke straal.

Hoeken aan de basis

De stelling zegt dat de hoeken zich bevinden opbasis van een gelijkbenige driehoek, zijn altijd gelijk. Het is heel eenvoudig om deze stelling te bewijzen. Beschouw de gelijkbenige driehoek ABC weergegeven, waarvoor AB = BC. Vanuit de hoek ABC is het nodig om een ​​bissectrice van de VD te tekenen. Beschouw nu de twee verkregen driehoeken. Door de voorwaarde AB = BC, is de zijde van de AP voor de driehoeken gebruikelijk, en de hoeken van de ABD en de SVD zijn gelijk, omdat VD de bissectrice is. Als we het eerste teken van gelijkheid noemen, kunnen we veilig concluderen dat de betreffende driehoeken gelijk zijn. En bijgevolg zijn alle overeenkomstige hoeken gelijk. En natuurlijk de feesten, maar op dit punt zullen we later terugkeren.

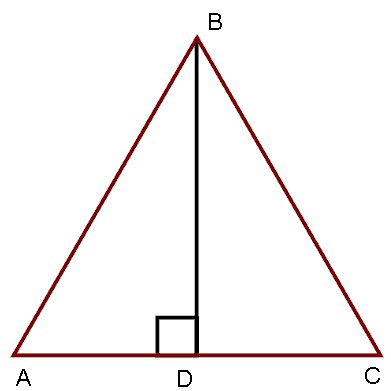
De hoogte van een gelijkbenige driehoek

De belangrijkste stelling waarop de oplossing is gebaseerdbijna alle problemen, klinkt als volgt: de hoogte in een gelijkbenige driehoek is een bissectrice en een mediaan. Om de praktische betekenis (of essentie) ervan te begrijpen, is het noodzakelijk om een ​​aanvullende uitkering te doen. Hiervoor is het noodzakelijk een gelijkbenige driehoek uit papier te verwijderen. De eenvoudigste manier om dit te doen is van een standaard tetrad-blad in de cel.

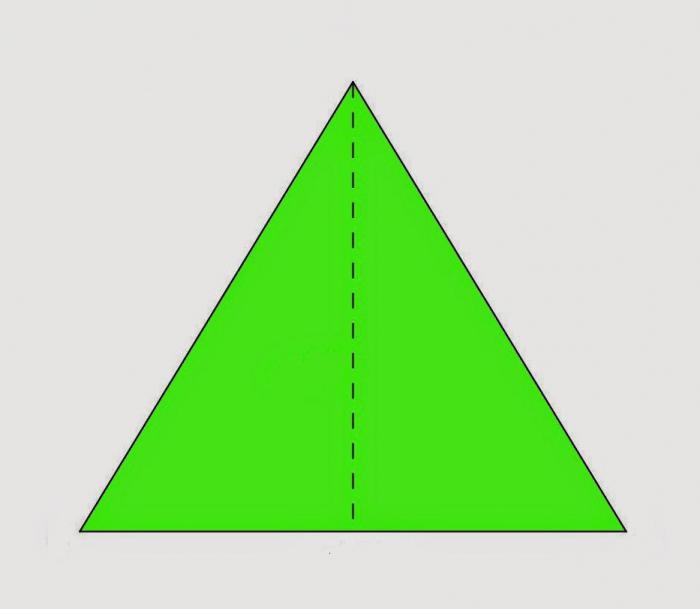
Vouw de resulterende driehoek dubbel, uitlijnendzijkanten. Wat is er gebeurd? Twee gelijke driehoeken. Nu moet je het giswerk controleren. Vouw de origami open. Teken een vouwlijn. Controleer met de hoekmeter de hoek tussen de getekende lijn en de basis van de driehoek. Wat zegt de hoek van 90 graden? Het feit dat de getrokken lijn loodrecht is. Per definitie - hoogte. Hoe de hoogte te vinden in een gelijkbenige driehoek, we hebben het uitgezocht. Laten we nu de hoeken aan de bovenkant behandelen. Controleer met dezelfde gradenboog de hoeken die nu door de hoogte zijn gevormd. Ze zijn gelijk. Dit betekent dat de hoogte ook een bissectrice is. Gewapend met een liniaal, meet de lengtes waarop de hoogte van de basis breekt. Ze zijn gelijk. Bijgevolg verdeelt de hoogte in een gelijkbenige driehoek de basis in twee en is een mediaan.

Bewijs van de stelling

Het visuele hulpmiddel toont duidelijk de waarheid van de stelling aan. Maar geometrie - wetenschap is vrij nauwkeurig, daarom is er bewijs voor nodig.

Tijdens de overweging van de gelijkheid van hoeken metde gelijkheid van driehoeken werd bewezen. Herinner dat de VD een bissectrice is en dat de driehoeken van de AVD en SVD gelijk zijn. De conclusie was: de overeenkomstige zijden van de driehoek en natuurlijk de hoeken zijn gelijk. Vandaar dat AD = SD. Daarom is VD de mediaan. Het blijft overblijven om te bewijzen dat VD een hoogte is. Uitgaande van de gelijkheid van de betreffende driehoeken, blijkt dat de hoek van de ADB gelijk is aan de hoek van de VDV. Maar deze twee hoeken zijn aaneengesloten en geven, zoals bekend, een totaal van 180 graden. Waar zijn ze dan aan gelijk? Natuurlijk, 90 graden. Dus, VD is de hoogte in een gelijkbenige driehoek getrokken naar de basis. Zoals vereist om te bewijzen.

Belangrijkste kenmerken

• Om problemen met succes op te lossen, is het noodzakelijk om de basisfuncties van gelijkbenige driehoeken te onthouden. Ze lijken tegengesteld aan de stellingen.
• Als in de loop van het oplossen van een probleem de gelijkheid van twee hoeken wordt gevonden, dan heb je te maken met een gelijkbenige driehoek.
• Als het mogelijk was om te bewijzen dat de mediaan tegelijk de hoogte van de driehoek is, concludeer dan vrijmoedig - de driehoek is gelijkbenig.
• Als de bissectrice ook de hoogte is, wordt de driehoek op basis van de hoofdkenmerken als gelijkbenig aangeduid.
• En, natuurlijk, als de mediaan in de rol van hoogte verschijnt, dan is zo'n driehoek gelijkbenig.

Hoogte formule 1

Voor de meeste problemen is het echter nodig om de rekenkundige hoogte te vinden. Daarom bekijken we hoe we de hoogte kunnen vinden in een gelijkbenige driehoek.

Laten we terugkeren naar de ABC-figuur hierboven, waarin a de zijkanten is en c de basis is. VD is de hoogte van deze driehoek, deze heeft de aanduiding h.

Wat is de driehoek van AED? Omdat VD de hoogte is, is de driehoek van de ABD rechthoekig, waarvan de cathet te vinden is. Met de formule van Pythagoras krijgen we:

AV² = АД² + ВД²

Nadat we uit de uitdrukking VD en uit de eerder gebruikte notatie hebben gekozen, verkrijgen we:

Н² = а² - (в / 2) ².

Het is noodzakelijk om de root te extraheren:

H = √²² - in² / 4.

Als we van het wortelteken ¼ verwijderen, ziet de formule er als volgt uit:

H = ½ √4a² - in².

Dit is de hoogte in een gelijkbenige driehoek. De formule volgt uit de stelling van Pythagoras. Zelfs als je deze symbolische invoer vergeet, dan kun je de methode van vinden altijd terugtrekken.

Hoogteformule 2

De hierboven beschreven formule is de belangrijkste en vakerHet wordt gebruikt voor het oplossen van de meeste geometrische problemen. Maar het is niet de enige. Soms wordt in de conditie, in plaats van de basis, de waarde van de hoek gegeven. Hoe kun je met dergelijke gegevens de hoogte in een gelijkbenige driehoek vinden? Om vergelijkbare problemen op te lossen is het raadzaam om een ​​andere formule te gebruiken:

H = a / sin α,

waar H de hoogte is die naar de basis is gericht,

maar - de zijkant,

α is de hoek aan de basis.

Als de taak de waarde van de hoek aan de top geeft, is de hoogte in de gelijkbenige driehoek als volgt:

H = a / cos (β / 2),

waar H de hoogte is die op de basis is gevallen,

β is de hoek bij de top,

a is de kant.

Rechthoekige gelijkbenige driehoek

Een zeer interessante eigenschap is de driehoek waarvan de top 90 graden is. Overweeg een rechthoekige driehoek ABC. Net als in de vorige gevallen is VD de hoogte die naar de basis is gericht.

De hoeken aan de basis zijn gelijk. Bereken hun geweldige werk zal niet zijn:

α = (180-90) / 2.

Dus de hoeken aan de basis,altijd 45 graden. Beschouw nu de driehoek ADV. Het is ook rechthoekig. Laten we de hoek van de ABD vinden. Door eenvoudige berekeningen krijgen we 45 graden. En bijgevolg is deze driehoek niet alleen rechthoekig, maar ook gelijkbenig. De partijen AD en VD zijn zijdelingse zijden en zijn onderling gelijk.

Maar de BP-zijde is tegelijkertijd de helftkant AC. Het blijkt dat de hoogte in een gelijkbenige driehoek de helft van de basis is en als we deze in de vorm van een formule schrijven, krijgen we de volgende uitdrukking:

H = B / 2.

Er moet aan worden herinnerd dat deze formule een exclusief geval is en alleen kan worden gebruikt voor rechthoekige gelijkbenige driehoeken.

Gouden driehoeken

Heel interessant is de gouden driehoek. In deze figuur is de verhouding van de laterale tot de basis gelijk aan de waarde die het Phidias-nummer wordt genoemd. De hoek aan de bovenkant is 36 graden, aan de basis - 72 graden. Deze driehoek werd bewonderd door de Pythagoreërs. De principes van de gouden driehoek vormen de basis van vele onsterfelijke meesterwerken. Bekend aan alle vijfpuntige sterren is gebouwd op de kruising van gelijkbenige driehoeken. Voor veel creaties gebruikte Leonardo da Vinci het principe van de 'gouden driehoek'. Compositie "Gioconda" is precies gebaseerd op de figuren die een regelmatige ster-pentagon creëren.

De afbeelding "Kubisme", een van de creaties van Pablo Picasso, fascineert het beeld dat in de basis van gelijkbenige driehoeken wordt gelegd.